CBSE- Squares and Square Roots-HOTS Questions
Class VIII Math
HOTS for Squares and Square Roots
HOTS for Squares and Square Roots
1. Find the square root of 144 by the method of repeated subtraction.
2. Find the smallest number by which 1800 must be multiplied so that it becomes a perfect square. Also find the square root of the perfect square so obtained.
3. Is 2352 a perfect square? if not, find the smallest number by which 2352 must be multiplied so that the product is a perfect square. Find the square root of new number.
4. The area of a square field is 8281 m2. Find the length of its side.
5. Find the square root of 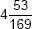
6. Simplify:
7. Factorise: p2 – 10p + 25.
8. 1225 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
9. Find the smallest number by which 3645 should be divided so as to get a perfect square. Also, find the square root of the number so obtained.
10. For each of the following numbers, find the smallest number by which we divide it so as to get a perfect square. Also find the square root of the square numbers so obtained.
(a) 37845
(b) 2800
(c) 45056
11. The students of Class VIII of a school donated Rs 2401 for Prime Minister��s National Relief Fund. Each student donated as many rupees as the number of students in the Class. Find the number of students in the Class.
12. There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement?
13. A school collected Rs 2304 as fees from its students. If each student paid as many paise as there were students in the school, how many students were there in the school?
14. 2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
15. 10404 students are sitting in a lecture room in such a manner that there are as many students in a row as there are rows in a lecture room. How many students are there in each row of a lecture room?
